The Causal Arrow in Little's Law
Why Little's Law matters in the "real world"
Most people think Little’s Law is about stability. But what it says about causality Is even more important.
This is the third post in our series of essays on Little’s Law here at The Polaris Flow Dispatch.
The first post, The Many Faces of Littles Law was our high level introduction to the key generalizations to Little’s Law that were made in the 50+ years since the original proof of a queueing theory result by Dr. John Little. Dr. Little’s result is the de-facto definition of Little’s Law and this post reviewed the generalizations made by researchers since that proof and explained why this was a much more relevant starting point for applications of Little’s Law in complex, dynamic, non-stationary environments like software product development.
The second post. A Brief History of Little’s Law was more in-depth examination of the history of the proofs and proof techniques that led to this modern understanding. Besides being a useful context to understand how these developments relate to each other, understanding the proof techniques gives us insights into why the law is true, which then helps us understand how to apply it in context.
All, this inevitably leads to the question - so what? Why should anyone in the “real world” care about any of this. Is this just abstract mathematical theory with no practical applications outside the lab?
The “real world” arguments, particularly in complex knowledge work domains like software development, is often tied to the popular conception of Little’s Law as a result that applies to stable, steady state systems - which “real world” systems often are not.
The first two posts were intended to broaden that framing so that it is clear that Little’s Law can be applied as-is to systems that are not stable, potentially expanding the scope of “real world” applications.
So the next question is how?
This post addresses that question conceptually before the rest of this series starts digging into more granular details of how to operationalize these ideas in software development in particular - where will need to deal with plenty of “real world” problems.
Little’s Law in the “real world”
The conventional story is that Little’s Law tells you when a system is stable. Since the law holds for stable systems, the thinking is that any system where it holds must be stable first. But if most “real world systems” are not stable, is the law even relevant?
There are three problems with this line of reasoning.
First, it ignores the fact that many systems that appear unstable when viewed on short timescales are in fact stable when viewed over sufficiently long timescales, and thus are directly amenable to analysis with Little’s Law. In this scenario, we can often rely on the fact that knowing any two of the values in the identity 𝐋 = 𝛌𝐖 gives us the third to apply the law in useful ways.
There are many useful “back-of-the-envelope” calculations that can be made where we can easily measure two of the variables and can estimate a third, harder to measure quantity.
As but one example, in software development, portfolio level average lead times can often be quite easily and accurately estimated by looking at how many things were planned and delivered over a sufficiently large number of quarters. This gives very reasonable estimates for strategic planning using available historical data without building expensive measurement infrastructure to track the granular details of projects and their detailed timelines.
There are many, many more applications in this vein and this is by far the most common use case for the law in general operations management 1.
Second, many real world system that are unstable, can be brought into a “quasi-stable” state by adopting process controls that actively manage 𝐋, 𝛌 and 𝐖. Much of Lean process engineering disciplines focus on this. So this opens up another avenue of applications for the stationary forms of Little’s Law.
Third, and arguably the most important, the law holds even in unstable and non-stationary systems, as we saw in the first two posts. So the fact that a system might be unstable does not rule out useful applications of the law.
So what are these applications?
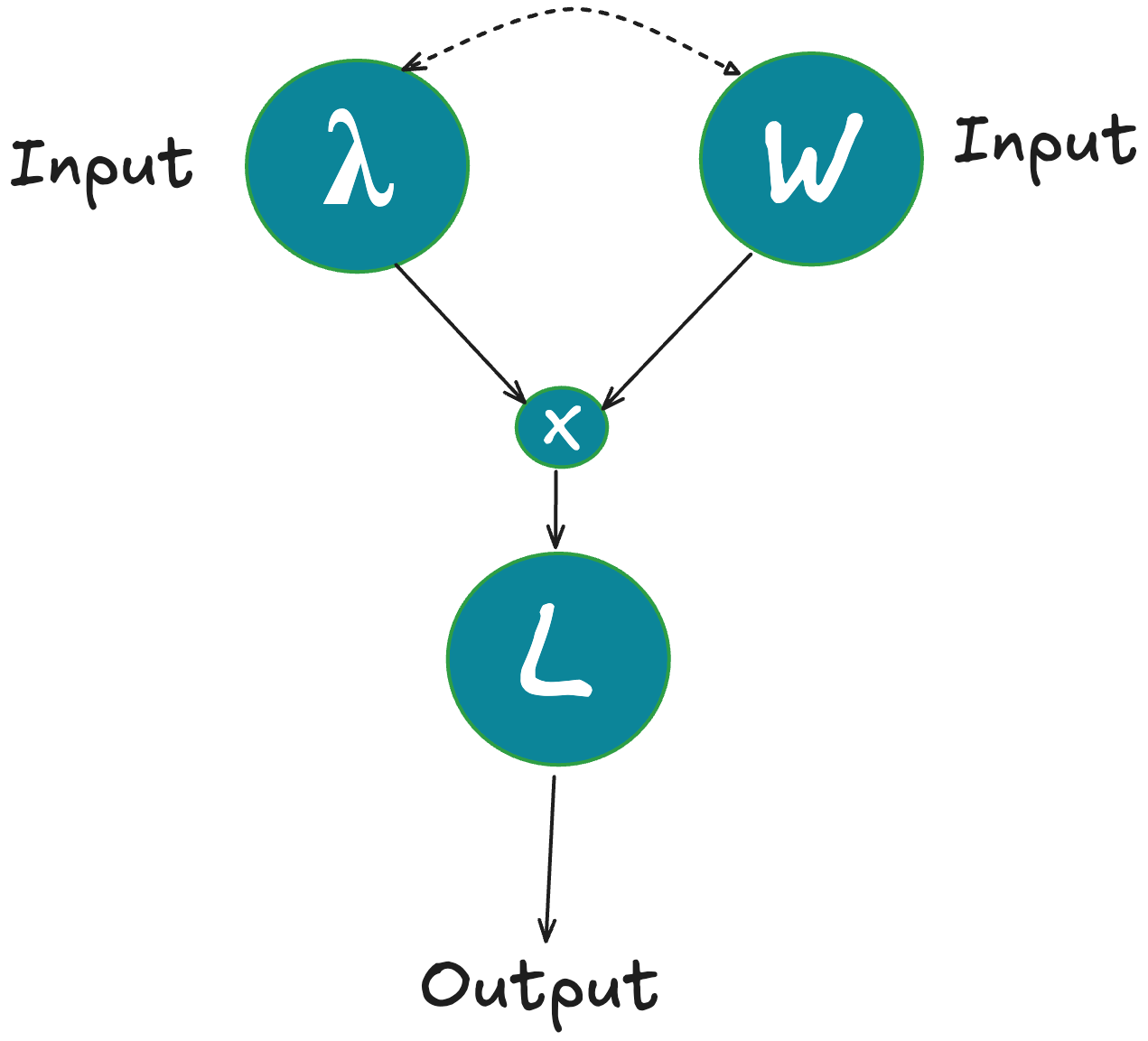
This gets us to what, in my view, is the most important reason why the law matters in the “real world”: whenever Little’s Law holds, it lets you reason about cause and effect when 𝐋, 𝛌 and 𝐖 change.
The Causal Mechanism
The identity 𝐋 = 𝛌𝐖 does more than link three averages via an equation, it encodes a causal structure: 𝐋 (time average of the number of items in system) is an output, determined by 𝛌 (arrival rate) and 𝐖 (average time items spend in system)2.
This defines the mechanics of Little's Law :
You can change 𝛌 or 𝐖, and this changes 𝐋. You cannot change 𝐋 directly.
Conversely, if you see that 𝐋 has changed, it must be because either or both of 𝛌 or 𝐖 changed and the new value of 𝐋 will be the product of the new values of 𝛌 and 𝐖.
This is a robust rule for causal inference but the causal relationship here is often misunderstood or mis-applied.
You’ll hear statements like: “Reducing WIP (𝐋)3 reduces cycle time (𝐖).”
Not really. The causal arrow doesn’t point that way4.
The law only says the three values are constrained by the equation. It does not tell you how 𝐖 will change in response to changes in 𝛌 or 𝐋.
Similarly, consider 𝐓𝐡𝐫𝐨𝐮𝐠𝐡𝐩𝐮𝐭 = 𝐖𝐈𝐏 ÷ 𝐂𝐲𝐜𝐥𝐞 𝐓𝐢𝐦𝐞.
It’s tempting to read this as a causal mechanism (shorten cycle time to increase throughput). But you can’t use it that way.
Two things are at play here:
The equality constraint: knowing any two values fixes the third and
The causal mechanism: 𝐋 changes when and only when 𝛌 or 𝐖 change.
Both are often used together in applications, but the latter is the only inference rule we can use for reasoning about cause and effect using Little’s Law.
𝐋 = 𝛌𝐖 is unambiguous.
It tells us: change the inputs (𝛌, 𝐖), and the output (𝐋) is determined. That’s the causal structure the law gives, and it’s the only one we can rely on.
It’s hugely important, but it holds only when 𝐋, 𝛌, and 𝐖 satisfy Little’s Law.
Again, so what?
Well, this sets the stage for us to begin operationalizing Little’s Law as systems analysis tool.
At a high level, this means: observe “a system” as a black box and measure 𝐋, 𝛌, and 𝐖 over consistent intervals where the identity 𝐋 = 𝛌𝐖 holds.
If we can do this, we don’t just have three disconnected numbers, we have a reliable mechanism for detecting changes in 𝐋 and analyzing its proximate causes (𝛌, 𝐖) without any additional internal info about the system.
If we cant, then there is a whole set of diagnostics that one can derive for why it does not. The proof techniques behind the law show us how.
Either way, this first-pass analysis using Little’s Law is going to be the starting point for a deeper causal analysis of flow in “a system” however you choose to define it: we can measure and monitor changes in 𝐋 and trace it back to changes in 𝛌 and 𝐖. This is a dynamic analysis enabled when 𝐋 = 𝛌𝐖 holds over the measurements.
Now when we see changes in 𝛌 and 𝐖, we can layer in additional info about the system into this black box view to explain these changes.
This is important because changing 𝛌 can change 𝐖 and vice versa, and these can jointly influence 𝐋 but that is not explainable by Little's Law alone. We need more details about the system.
Typically this is where queueing theory comes in the classical operations management applications of Little’s Law. We gather information about probability distributions, service policies, capacity, concurrency, service rates, utilization etc. to the extent they are measurable to able to understand the dynamics of the relationship between 𝛌 and 𝐖.
Or we may forgo queueing theory altogether and use heuristic models like the Theory of Constraints if detailed measurements are not possible.
In complex domains free form narratives5, value stream maps, collaboration protocols, etc. all play a role in building a deeper understanding why the system behaves as it does. Quantitatively, these translate into context we can bring to explain how 𝛌 and 𝐖 interact.
The key thing that Little’s Law enables is a clean separation between a “black box” view of a system where we can make meaningful causal inferences about changes in the system without knowing any of the details of the system other than the observable variables 𝐋, 𝛌, and 𝐖.
When modeling systems this way, the definition of the boundaries of the “black box” and even the “items” that are under analysis are up to the modeler. Little’s Law is agnostic to all this.
This allows to to decompose “the system” from an outside-in view to whatever level of detail that makes sense for answering the questions that the analyst is interested in. There is no single defined way of decomposing a “system” up front - we choose the perspectives and granularity and timescales over which we are interested in performing the analysis.
In short, when they satisfy Little’s Law 𝐋, 𝛌 and 𝐖 are 𝐚𝐜𝐭𝐢𝐨𝐧𝐚𝐛𝐥𝐞. Not every combination of WIP, cycle time, or throughput numbers can claim that.
And this is why Little’s Law matters in the “real world”.
Up next
Starting with the next post in the series, we will start making all this concrete with a more detailed description of how to do this type of operationalization in practical software development contexts.
We’ll start with showing how to produce accurate and actionable 𝐋, 𝛌 and 𝐖 for systems of interest.
One of the remarkable things is that, given the generality of Little’s Law, this is almost always possible once you’ve focused on what problems you are trying to solve for and established a clear working context for the observations. Even understanding clearly why Little’s Law doesn’t apply gives useful insights that are actionable.
But you’ll need the background in the first two posts to fully make sense of the details in the rest of the series, so if you have not read those yet, this would be a great time to catch up before we dive into deeper waters.
If you are interested in receiving these updates in your inbox as they are published please subscribe for updates.
The 2011 survey article on Little’s Law by Dr. Little has many such examples. They are useful to study, not just for the specific applications, but also to understand the types of reasoning you can do with Little’s Law. Those reasoning modes are what let you apply it laterally across domains.
To understand why this is, it helps to understand the formal definitions and proof techniques behind the law. The first two posts in the series should help, as will the details in the posts coming up in this series.
Leave aside for now the technical detail that L is a time average of instantaneous WIP and when people say WIP they often mean instantaneous WIP. The arguments here hold even if the technically “correct” interpretation of WIP is used.
Let’s say we throttle arrivals (lower 𝛌) - this is one mechanism to potentially reduce 𝐋 since you cant change it directly. But even assuming that the equation in Little’s Law holds, that equation alone still doesn’t guarantee that reducing 𝛌 will change 𝐋 or 𝐖 in a predictable way. And even if it did, it is not reducing 𝐋 that causes 𝐖 to fall, so the causal inference here is wrong.
In software development in particular, the importance of narratives in providing context for understanding cause and effect relationships between 𝛌 and 𝐖 cannot be overstated. Many of the parameters we need to apply classical queueing theory to software development are not easy or even impossible to measure directly.
But specific narratives around teams and team topologies, engineering processes, technical architecture, collaboration styles etc. give us the very plausible hypotheses for explaining dynamics of 𝛌 and 𝐖 in ways we can measure and test rigorously using Little’s Law.
So while queueing theory is often useful in this context, it needs to be combined with a qualitative and contextual information in order to make useful decisions. We will have more to say on this later in this series.